现在我们用堆栈解决一个有意思的问题,定义一个二维数组:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的路线。程序如下:
例 12.3. 用深度优先搜索解迷宫问题
#include <stdio.h>
#define MAX_ROW 5
#define MAX_COL 5
struct point { int row, col; } stack[512];
int top = 0;
void push(struct point p)
{
stack[top] = p;
top++;
}
struct point pop(void)
{
top--;
return stack[top];
}
int is_empty(void)
{
return top == 0;
}
int maze[MAX_ROW][MAX_COL] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
void print_maze(void)
{
int i, j;
for (i = 0; i < MAX_ROW; i++) {
for (j = 0; j < MAX_COL; j++)
printf("%d ", maze[i][j]);
putchar('\n');
}
printf("*********\n");
}
struct point predecessor[MAX_ROW][MAX_COL] = {
{{-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}},
{{-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}},
{{-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}},
{{-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}},
{{-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}, {-1,-1}},
};
void visit(int row, int col, struct point pre)
{
struct point visit_point = { row, col };
maze[row][col] = 2;
predecessor[row][col] = pre;
push(visit_point);
}
int main(void)
{
struct point p = { 0, 0 };
maze[p.row][p.col] = 2;
push(p);
while (!is_empty()) {
p = pop();
if (p.row == MAX_ROW - 1 /* goal */
&& p.col == MAX_COL - 1)
break;
if (p.col+1 < MAX_COL /* right */
&& maze[p.row][p.col+1] == 0)
visit(p.row, p.col+1, p);
if (p.row+1 < MAX_ROW /* down */
&& maze[p.row+1][p.col] == 0)
visit(p.row+1, p.col, p);
if (p.col-1 >= 0 /* left */
&& maze[p.row][p.col-1] == 0)
visit(p.row, p.col-1, p);
if (p.row-1 >= 0 /* up */
&& maze[p.row-1][p.col] == 0)
visit(p.row-1, p.col, p);
print_maze();
}
if (p.row == MAX_ROW - 1 && p.col == MAX_COL - 1) {
printf("(%d, %d)\n", p.row, p.col);
while (predecessor[p.row][p.col].row != -1) {
p = predecessor[p.row][p.col];
printf("(%d, %d)\n", p.row, p.col);
}
} else
printf("No path!\n");
return 0;
}运行结果如下:
2 1 0 0 0 2 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0 ********* 2 1 0 0 0 2 1 0 1 0 2 0 0 0 0 0 1 1 1 0 0 0 0 1 0 ********* 2 1 0 0 0 2 1 0 1 0 2 2 0 0 0 2 1 1 1 0 0 0 0 1 0 ********* 2 1 0 0 0 2 1 0 1 0 2 2 0 0 0 2 1 1 1 0 2 0 0 1 0 ********* 2 1 0 0 0 2 1 0 1 0 2 2 0 0 0 2 1 1 1 0 2 2 0 1 0 ********* 2 1 0 0 0 2 1 0 1 0 2 2 0 0 0 2 1 1 1 0 2 2 2 1 0 ********* 2 1 0 0 0 2 1 0 1 0 2 2 0 0 0 2 1 1 1 0 2 2 2 1 0 ********* 2 1 0 0 0 2 1 0 1 0 2 2 2 0 0 2 1 1 1 0 2 2 2 1 0 ********* 2 1 0 0 0 2 1 2 1 0 2 2 2 2 0 2 1 1 1 0 2 2 2 1 0 ********* 2 1 2 0 0 2 1 2 1 0 2 2 2 2 0 2 1 1 1 0 2 2 2 1 0 ********* 2 1 2 2 0 2 1 2 1 0 2 2 2 2 0 2 1 1 1 0 2 2 2 1 0 ********* 2 1 2 2 2 2 1 2 1 0 2 2 2 2 0 2 1 1 1 0 2 2 2 1 0 ********* 2 1 2 2 2 2 1 2 1 2 2 2 2 2 0 2 1 1 1 0 2 2 2 1 0 ********* 2 1 2 2 2 2 1 2 1 2 2 2 2 2 2 2 1 1 1 0 2 2 2 1 0 ********* 2 1 2 2 2 2 1 2 1 2 2 2 2 2 2 2 1 1 1 2 2 2 2 1 0 ********* 2 1 2 2 2 2 1 2 1 2 2 2 2 2 2 2 1 1 1 2 2 2 2 1 2 ********* (4, 4) (3, 4) (2, 4) (1, 4) (0, 4) (0, 3) (0, 2) (1, 2) (2, 2) (2, 1) (2, 0) (1, 0) (0, 0)
这次堆栈里的元素是结构体类型的,用来表示迷宫中一个点的x和y座标。我们用一个新的数据结构保存走迷宫的路线,每个走过的点都有一个前趋(Predecessor)的点,表示是从哪儿走到当前点的,比如predecessor[4][4]是座标为(3, 4)的点,就表示从(3, 4)走到了(4, 4),一开始predecessor的各元素初始化为无效座标(-1, -1)。在迷宫中探索路线的同时就把路线保存在predecessor数组中,已经走过的点在maze数组中记为2防止重复走,最后找到终点时就根据predecessor数组保存的路线从终点打印到起点。为了帮助理解,我把这个算法改写成伪代码如下:
将起点标记为已走过并压栈;
while (栈非空) {
从栈顶弹出一个点p;
if (p这个点是终点)
break;
否则沿右、下、左、上四个方向探索相邻的点,if (和p相邻的点有路可走,并且还没走过)
将相邻的点标记为已走过并压栈,它的前趋就是p点;
}
if (p点是终点) {
打印p点的座标;
while (p点有前趋) {
p点=p点的前趋;
打印p点的座标;
}
} else
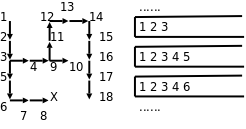
没有路线可以到达终点;我在while循环的末尾插了打印语句,每探索一步都打印出当前标记了哪些点,从打印结果可看出这种搜索算法的特点:每次取一个相邻的点走下去,一直走到无路可走了再退回来,取另一个相邻的点再走下去。这称为深度优先搜索(DFS,Depth First Search)。探索迷宫和堆栈变化的过程如下图所示。
图中各点的编号反映出探索的顺序,堆栈中的数字就是图中点的编号,可见正是因为堆栈后进先出的性质使这个算法具有了深度优先的特点。如果在探索问题的解时走进了死胡同,则需要退回来从另一条路继续探索,这种思想称为回溯(Backtrack),一个典型的例子是很多编程书上都会讲的八皇后问题。
最后我们打印终点的座标并通过predecessor数据结构找到它的前趋,这样顺藤摸瓜一直打印到起点。那么能不能从起点到终点正向打印路线呢?在上一节我们看到,如果是在一个循环里打印数组,既可以正向打印也可以反向打印,因为数组这种数据结构是支持随机访问的,当然也支持顺序访问,并且既可以是正向的也可以是反向的。但现在predecessor这种数据结构的每个元素只知道它的前趋是谁,而不知道它的后继(Successor)是谁,所以在循环里只能反向打印。由此可见,有什么样的数据结构就决定了可以用什么样的算法。那么,为什么不再建一个successor数组来保存每个点的后继呢?虽然每个点的前趋只有一个,后继却不止一个,从DFS算法的过程可以看出,如果每次在保存前趋的同时也保存后继,后继不一定会指向正确的路线,请读者想一想为什么。由此可见,有什么样的算法就决定了可以用什么样的数据结构。设计算法和设计数据结构这两件工作是紧密联系的。